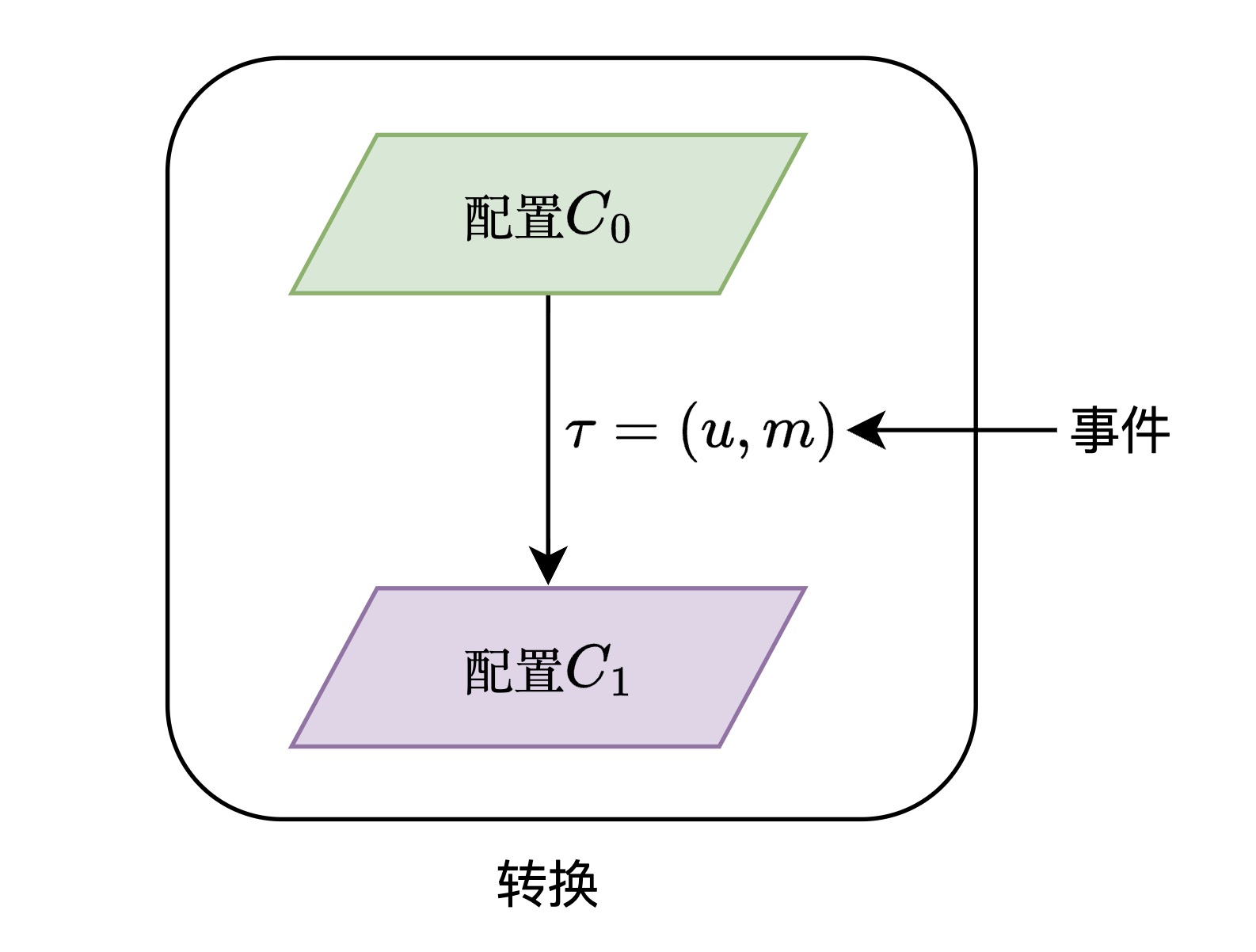
当进程 接收到了一个消息 ,从而使系统从配置 变为 ,则称 为一个事件,且称该过程为一个转换。
简要证明
在完全异步的模型下,即使只允许一个进程失败,也没有任何算法能够保证达成共识。
分布式系统配置
假设我们的系统中共有5台计算机,每台计算机内运行一个进程。
5个进程所处的状态以及已发送到网络中但未被接收的消息,合称为系统的配置:
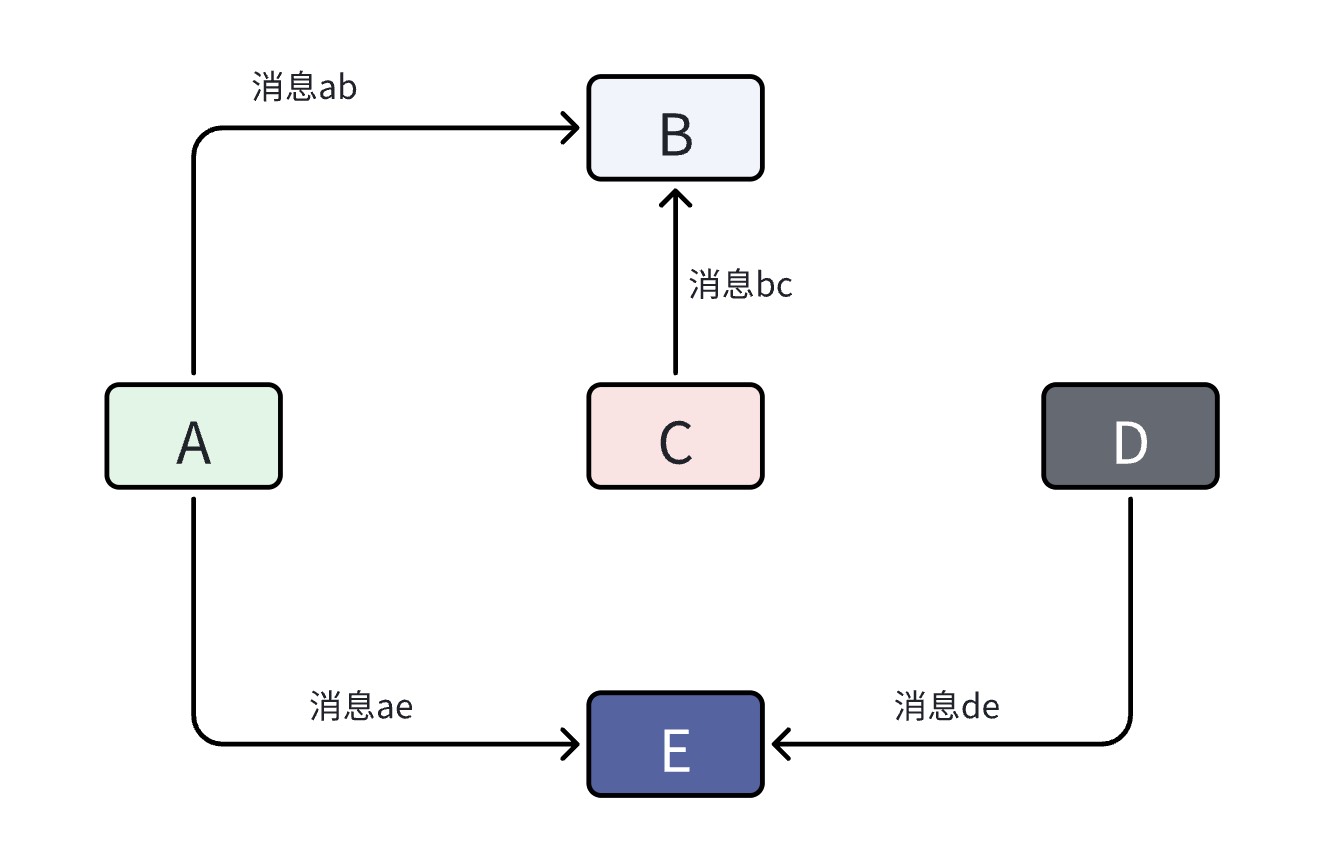
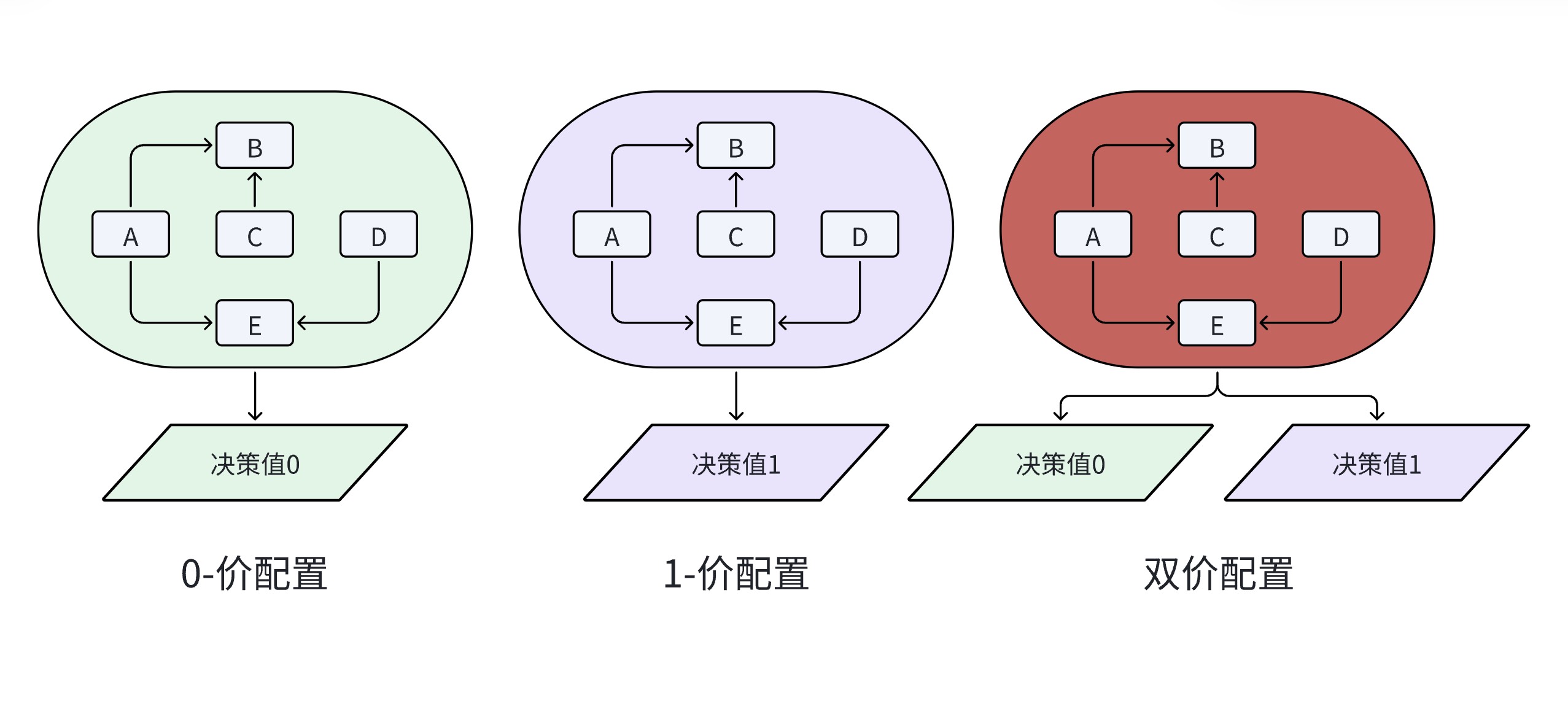
如果当前系统处于某个配置下:
- 最终决策值一定为
0,则称该配置为0-价配置 - 最终决策值一定为
1,则称该配置为1-价配置 - 最终决策值可能为
0,也可能为1,具体需要看消息的传递情况以及进程的执行情况。此时称该配置为二价配置
事件与转换
定义:事件与转换
关键配置
定义:关键配置
对于一个二价配置,如果经过一个单一转换后的配置全都是单价的,则称该二价配置为一个关键配置。
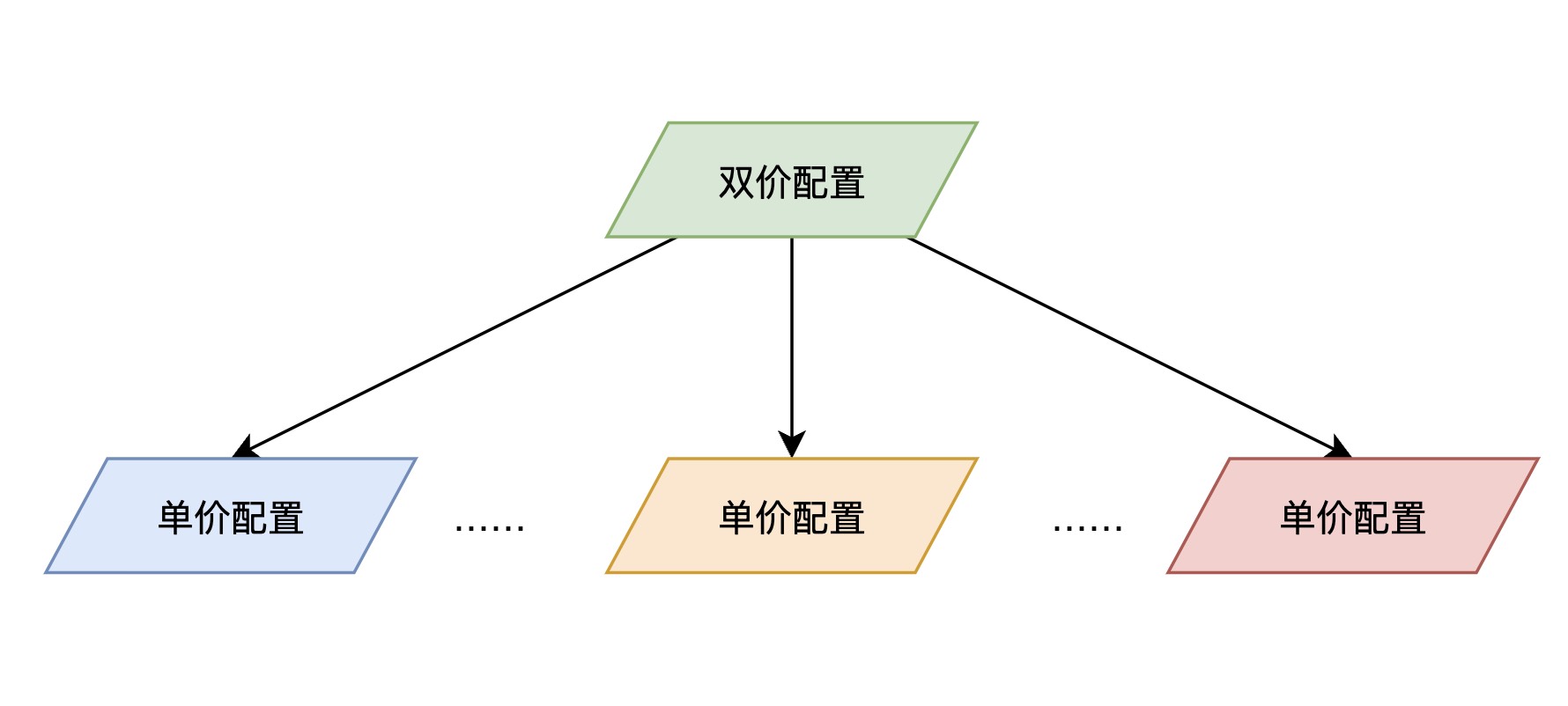
系统一旦进入关键配置,则意味着系统接下来一定能够达成共识。
证明思路
我们证明的思路是:
- 先证明如果允许至少一个进程崩溃,则系统必然存在一个初始的二价配置,而系统一旦进入一个二价配置,想要保证
一定能够达到共识,则系统必须能够在有限的时间内进入关键配置 - 再证明当系统处于
关键配置时,存在单一进程的崩溃,会使得系统陷入僵持状态,无法达成共识
我们还是用配置树示例:
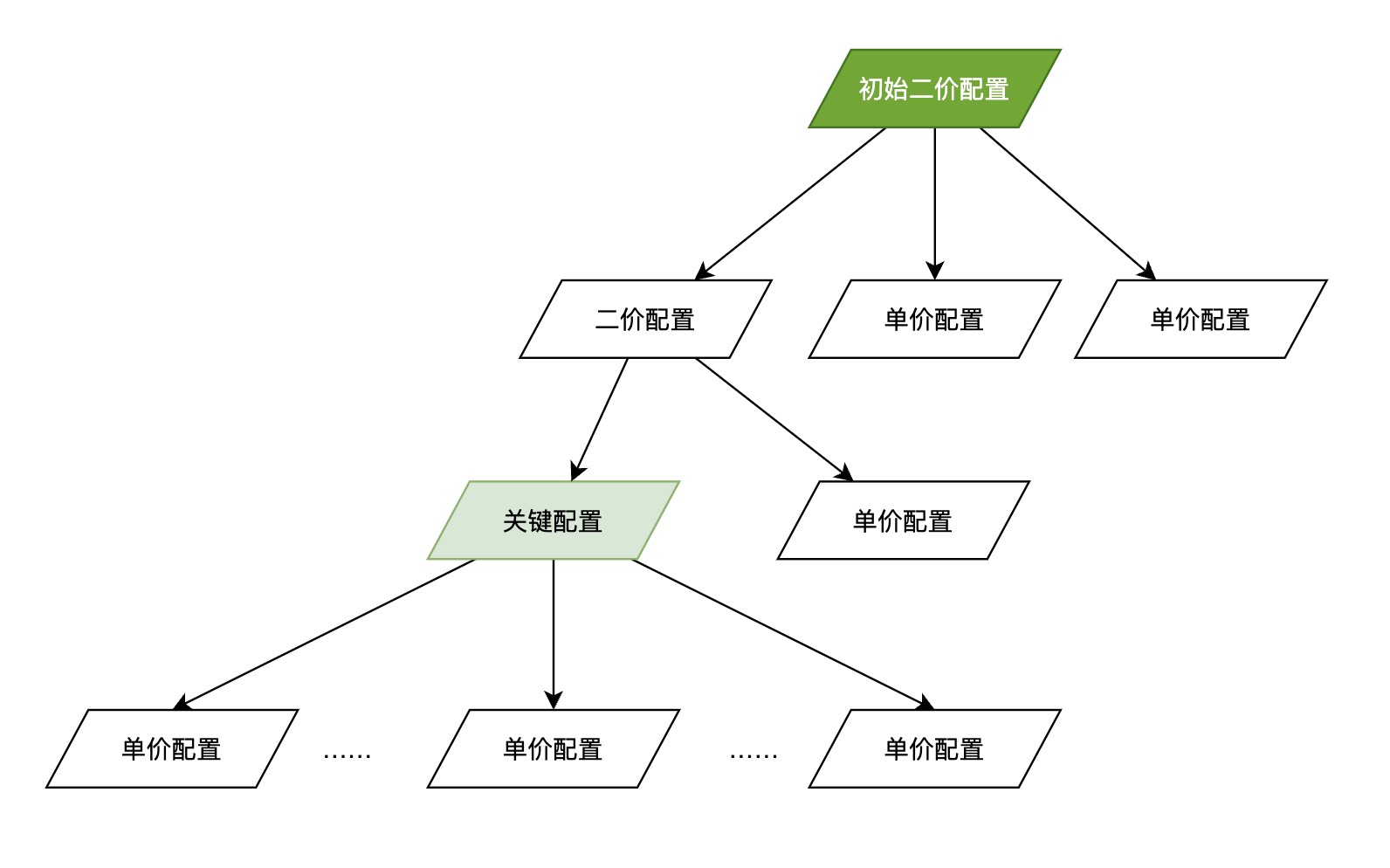
首先,既然算法宣称能够达成共识,则当系统从一个初始二价配置开始的话,算法最终也应当能够达成共识。
当系统进入了一个二价配置,算法要保证一定能够达成共识,那么就需要在有限的时间内进入一个关键配置。例如,如果初始二价配置不是关键配置(如上所示),那么它必然有一个二价配置的子结点,而该二价配置如果不是关键配置,则它也必然有一个二价配置的子结点,如果一直没有到达一个关键配置,则该过程会无限重复下去,系统永远达不到共识。
最后,我们证明如果系统确实在有限时间内进入了一个关键配置,则必然存在一个进程,该进程的崩溃,使得系统陷入僵持状态而无法达成共识。从而完成证明。
引理1
引理1
如果允许至少一个进程崩溃,则系统必然存在一个初始的二价配置
对于初始配置而言,由于系统处于初始状态,则系统中并没有正在传输的消息,因此一个初始配置实际上相当于每一个进程的输入值的集合。在我们的模型中,进程的输入值即0或1,相当于每一个进程在算法一开始时希望提议的决策值。
那么最终达成共识的决策值,必须从这个输入值集合中选出。例如,如果5个进程都提议0,我们记作V[0, 0, 0, 0, 0],则最终决策值显然只能为0,同样的,如果5个进程都提议1,记作V[1, 1, 1, 1, 1],则最终决策值显然只能为1。
为了证明引理1,我们使用反证法。假设系统所有的初始配置都是单价配置。
考虑以下6组输入值,按照假设,他们都是单价配置:
推论
由于最终决策值为0,而最终决策值为1。那么必然相邻的两个输入值,其中的决策值为0,而的决策值为1,并且与之间的不同,仅仅在于号进程的输入值不同。
例如,从开始,必定是0-价配置。检查,如果是1-价配置,那么我们就找到了:,之间输入值的不同,仅仅是1号进程的输入值不同。
如果也是0-价配置,则接着检查。如果一直都是0-价配置,则一直到处,如果仍是0-价配置,而本身又必然是1-价配置,那么我们就找到了:,之间输入值的不同,仅仅是5号进程的输入值不同。
与之间,仅仅在于号进程的输入值不同,如果该进程宕机,则剩余其他进程的输入值是完全相同的,那么系统最终的决策值应该是0还是1呢?
如果最终是0,而实际上初始配置可能是1-价配置的;如果最终是1,而实际上初始配置可能是0-价配置的。因而导出矛盾。原假设不成立,因而系统必然有一个双价初始配置。
引理2
引理2
当系统进入一个二价配置,想要保证达到共识,则系统必须在有限时间内达到一个关键配置
该引理是显而易见的。当系统进入一个二价配置,如果该二价配置不是关键配置,意味着它还有一个二价配置的子结点。系统就有可能通过一个转换进入该二价配置,如果该二价配置还不是关键配置,则又意味着它还有一个二价配置的子结点……该过程可以一直持续,使系统永远达不到共识。
引理3
引理3
假设有两个转换,都可以应用在配置上。表示先应用,后应用,表示先应用,后应用。则
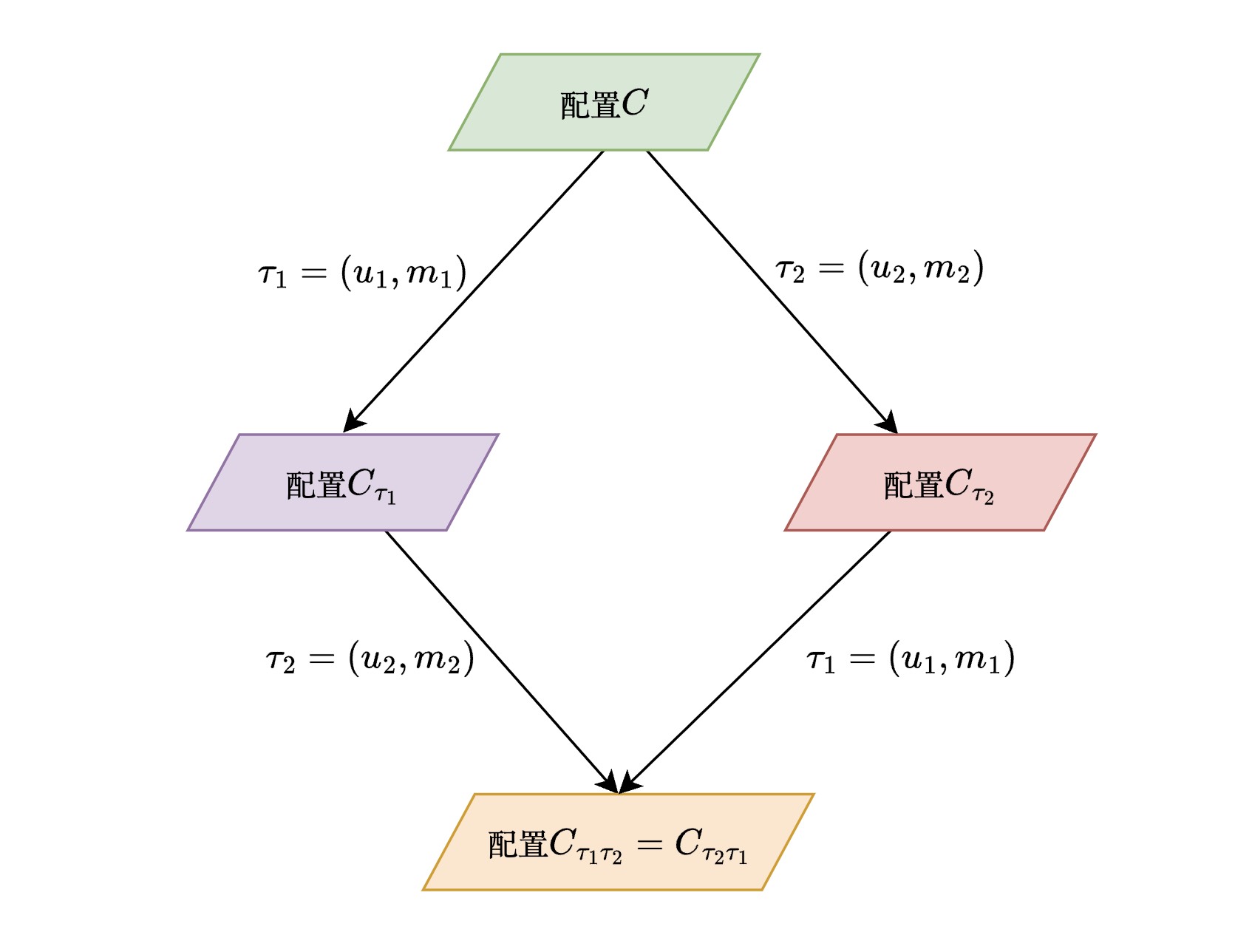
证明: 该引理实际上是显而易见的。与是独立的两个进程,且独立应用于,而独立应用于。因而这两个转换是完全独立的,它们最终消耗同样的消息,导致同样的状态转换,且产生同样的新的待传递消息。因而最终结果 与也相等。
引理4
引理4
当系统处于关键配置,则存在某个进程,其宕机会使得系统陷入僵持状态,无法达成共识
假设系统当前处于关键配置,则可应用于配置的转换集合中,必然存在有,其中使关键配置转到0-价配置,使关键配置转到1-价配置(是关键配置,因此必定存在这两个转换)。
如果与不是同一个进程,则根据引理3,我们对应用,根据顺序不同,可以得到:
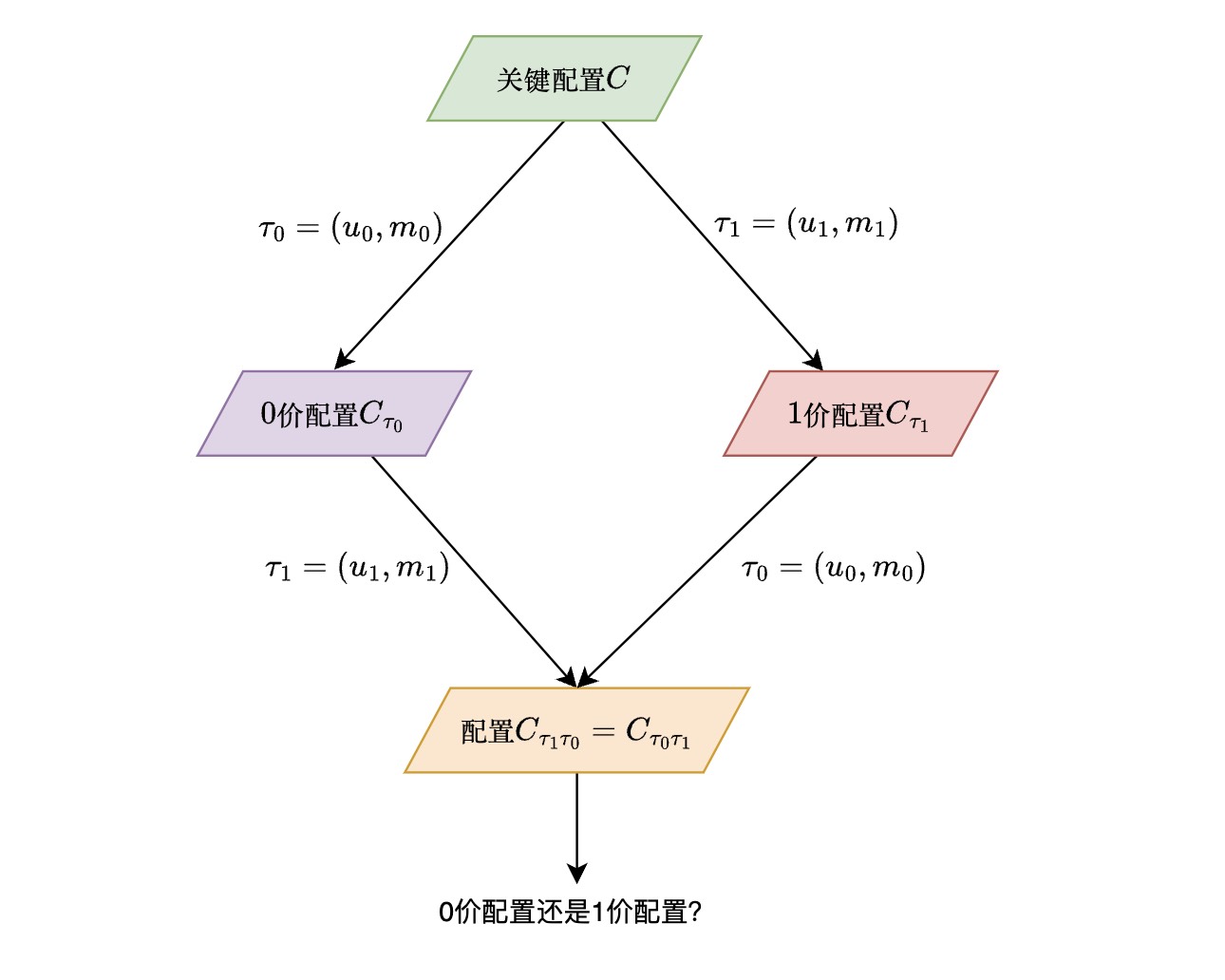
由于先应用了,因此应当为0价配置,其后继配置也是0价配置。同理,应当是1价配置。这就与相矛盾。因此,。
对于可以应用于配置的转换集合,可以分为将转为0价配置的转换子集,以及将转为1价配置的转换子集。那么对于任意的,都满足以上论证。因此,转换集合中的所有转换,实际上都是同一个进程的转换!
如果此时进程宕机,则系统永远无法进入一个单价配置,从而无法达到共识。引理4证毕。
最终证明
FLP不可能性定理
在完全异步的模型下,即使只允许一个进程失败,也没有任何算法能够保证达成共识
证明:由引理1可知系统必然存在一个初始二价配置,由引理2可知系统要能保证达到共识,则当系统处于初始二价配置时,必须在有限时间内达到一个关键配置,而由引理4,又可知当系统处于关键配置时,必然能找到一个进程,该进程宕机使系统永远无法进入一个单价配置,从而永远无法达到共识。
FLP不可能性定理证明完毕。